FEE question paper solved section 1 2019
FUNDAMENTALS OF ELECTRICAL ENGINEERING, 2019
paper solved.
Q.1 (a) Select the most appropriate option: (Each of one
mark)
1. With Ohm's law, if voltage increases and resistance stays
the same:
a. Current Remains the Same
b. Power Decreases
c. Current Increases
d. Resistance Decreases
Ans: C
2. KCL is based on the fact that_______.
a. There cannot be an accumulation of charge at a node.
b. There is a possibility for a node to store energy.
c. Charge accumulation is possible at node
d. Charge accumulation may or may not be possible.
Ans :B
3. A battery is made by combination of 6 cells in series,
each capable of
delivering 4 ampere at 2V. How much voltage and current can
it
deliver?
a. 12V and 24A
b. 2V and 24A
c. 12V and 4A
d. 2V and 4A
Ans:C
4. Capacitance of a parallel plate capacitor decreases
by_______.
a. Increasing the area of plates
b. Increasing the distance between the plates
c. Putting a dielectric between the plates
d. Decreasing the distance between the plates
Ans:B
5. The strength of a magnetic field around an infinite
current carrying
conductor is_______.
a. Directly proportional to the distance
b. Same every where
c. Inversely proportional to the distance
d. Inversely proportional to the square of the distance
Ans:C
6. M.M.F is analogous to_______.
a. Electric current in electric circuit
b. Current density in conductor
c. Electromotive force
d. Voltage
Ans:C
(b) Answer following questions: (Each of two mark) 10
1. Define following terms:
1) Node 2) Junction
Node : The point through which
an circuit element is connected to the circuit is called Node
Here point
A,B,C and D is called Node
Ans:Any point in an electric circuit where two
or more conductors are joined together is a junction.
2. Justify the statement: Capacitor can store more energy
if the size of
the capacitor plates is larger but the distance between
them is
smaller.
Ans : We know, C=ϵ⋅A/d,
This relation show
that when the when the distance between two plate is lesser
the capacitance is greater and capacitance is directly proportional to area
of each plate.
3. Draw star-delta configurations. Mention the
expressions for star-
delta transformations.
Ans:
4. Show the application of Kirchoff’s current law in an
electrical circuit
with suitable example.
Ans: It states that the sum of
the currents flowing towards a junction is equal to the sum of currents leaving
the junction.
This is in accordance with the
conservation of charge which is the basis of Kirchhoff's current rule.
1.The Wheatstone bridge is an essential application of
Kirchhoff's laws
2.It is also used in mesh and node analysis
5. Define Permeance.
Ans: Permeance is defined as a measure of the ease with
which Magnetic Flux can be admitted
through a material or Magnetic circuit. Permeance is the reciprocal of reluctance. Permeance is directly proportional to the magnetic
flux. Its unit is Wb/AT or
Henry.
Q.2 (a) Define term: Hysteresis. Sketch
and explain hysteresis loop in detail. 06
Ans: The meaning of hysteresis is ”lagging”. Hysteresis is characterized as a lag of magnetic
flux density (B) behind the magnetic field strength (H).
Looking at the graph, if B is measured for various
values of H and if the results are plotted in graphic forms then the graph will
show a hysteresis loop.
- The magnetic flux density (B) is increased
when the magnetic field strength(H) is increased from 0 (zero).
- With increasing the magnetic field there is an
increase in the value of magnetism and finally reaches point A which is
called saturation point where B is constant.
- With a decrease in the value of the magnetic
field, there is a decrease in the value of magnetism. But at B and H are
equal to zero, substance or material retains some amount of magnetism is
called retentivity or residual magnetism.
- When there is a decrease in the magnetic field
towards the negative side, magnetism also decreases. At point C the
substance is completely demagnetized.
- The force required to remove the retentivity of
the material is known as Coercive force (C).
- In the opposite direction, the cycle is continued
where the saturation point is D, retentivity point is E and coercive force
is F.
- Due to the forward and opposite direction
process, the cycle is complete and this cycle is called the hysteresis
loop.
(b) Give the significance of following
terms:
1. Current
Ans: Current
is the rate at which electrons flow past a point in a complete electrical
circuit.
2. Potential difference:
Ans : Potential difference is the work done in moving a unit of
positive electric charge from one point to another.
The symbols for potential difference is V
3. Conductance
Ans: The reciprocal of
resistance (G = 1/R).
The conductivity is a measure of the susceptibility of a
material to the flow of electric current.
4. Electrical Power
Ans: Electric power is the rate at which
work is done or energy is transferred in an electrical circuit.
5. Electrical Energy
Ans: Electrical energy is the energy derived from electric potential energy or kinetic
energy of the charged particles
(c)
Compare the characteristics of magnetic circuits and electric circuits.
Ans Electric
Circuit and Magnetic Circuit
|
# |
Content |
Electrical Circuit |
Magnetic Circuit |
|
01 |
Basic Difference |
In an electrical circuit, electric
current flows through the closed path. |
In the magnetic circuit, magnetic
flux flows through the closed path. |
|
02 |
Definition of electric current & magnetic flux |
The number of free electrons or electric
charge particles that move in the circuit is called ‘Electric Current (I)‘. |
The number of magnetic lines of the
force passing through a magnet is called ‘Magnetic Flux (ɸ)’. |
|
03 |
Unit of current & flux |
Electric current is measured in Ampere
(A). |
Magnetic flux is measured in Weber (Wb). |
|
04 |
Circuit Role of electricity and magnetism |
In an electrical circuit, electric
current flows from positive
to negative polarities. |
In the magnetic circuit, magnetic flux
flows from N-pole
to S-pole. |
|
05 |
Difference between electric
force and magnetic force |
In an electrical circuit, an
electromotive force (EMF) is used to produce the electric current. |
In the magnetic circuit, magnetomotive
force (MMF) is used to produce the magnetic flux. |
|
06 |
Unit of EMF & MMF |
EMF is measured in ‘Volt (V)’. |
MMF is measured in ‘Ampere-turn (AT)’. |
|
07 |
Opposition |
In an electrical circuit, the resistance (R) opposes the flow of electric
current. |
In the magnetic circuit, the reluctance
(S) opposes the flow of magnetic flux. |
|
08 |
Unit of resistance &
reluctance |
The SI unit of resistance is ‘Ohm (Ω)’ |
The SI unit of reluctance is ‘Ampere-
turn/Weber (AT/Wb)’ |
|
09 |
Flowing Property of circuits |
Conductance (G) is the
reciprocal of the resistance. |
Permeance (P) is the reciprocal of
reluctance. |
|
10 |
Unit of conductance &
permeance |
Conductance is measured in ‘Siemens
(S)’. |
Permeance is measured in
‘Weber/Ampere-turn (Wb/AT)’ or ‘Henry (H)’ |
|
11 |
According to Ohm’s law of an electrical
circuit is, |
According to Ohm’s law of the magnetic
circuit is |
|
|
12 |
Kirchhoff’s Circuit Laws |
For the electrical circuit, Kirchhoff current law (KCL) and Kirchhoff voltage law (KVL) are
applicable. |
For magnetic circuit, Kirchhoff MMF law
and Flux law are applicable. |
|
13 |
Kirchhoff’s first law |
According to Kirchhoff’s first law of an
electrical circuit is, |
According to Kirchhoff’s first law of
the magnetic circuit is, |
|
14 |
Kirchhoff’s second law |
According to Kirchhoff’s second law of
an electrical circuit is, |
According to Kirchhoff’s second law, of
the magnetic circuit is, |
|
15 |
Current density & flux
density |
Current density (δ) is the rate of
the electric currents flowing per unit cross-sectional area of a
material. |
Flux density (B) is the rate of the
magnetic fluxes flowing per unit cross-sectional area of a material. |
|
16 |
Unit of the current &
flux density |
The current density of an electrical
circuit is measured in ‘Ampere/square*meter (A/m*m)’. |
The flux density of a magnetic circuit
is measured in ‘Weber/square*meter (Wb/m*m)’ or ‘Tesla (T)’. |
|
17 |
Field intensity of electrical
& magnetic circuits |
Electric field strength is the
electromotive force per unit electric charge. |
Magnetic field strength is the
magnetomotive force per unit length. |
|
18 |
Unit of electric &
magnetic field intensity |
The SI unit of the electric
field intensity is ‘Newton/Coulomb (N/C)’ or ‘Volt/Meter (V/m)’. |
The SI unit of the magnetic
field intensity is ‘Ampere/Meter (A/M)’ |
|
19 |
Circuit Structure |
The electrical circuit can be a closed
circuit or an open circuit. |
The magnetic circuit is always a
closed circuit. |
Write any 7 point
OR
Q.2 (a) Explain the following
(i) Primary Cells
Ans: A primary cell or battery is
the one that cannot easily be recharged after one use, and are discarded
following discharge. These cells are not
chargeable because the electrode reaction occurs only once and after the use
over a period of time the batteries become dead and cannot be reused.
(ii) Secondary Cells
Ans: A secondary cell or battery is one that can be electrically
recharged after its complete discharge. It is recharged by passing current
through the circuit in the opposite direction to the current during discharge.
(iii) Dry Cells
Ans: A cell in which
the electrolyte exists in the form of a paste, is absorbed in a porous medium,
or is otherwise restrained from flowing.
(iv) Sealed rechargeable cells
Ans: Cells that are
free from routine maintenance and can be operated without regard to position.
(b Mention the factors affecting resistance). Also,
describe the effect of
temperature on resistance for pure metals, alloys,
semi-conductors
and insulators.
Ans: Factor affecting resistance are:
· Resistance is proportional to length. ...
· Resistance is inversely
proportional to cross-sectional-area. ...
· Resistance depends on the
material the wire is made of. ...
· Resistance increases with
the temperature of the wire.
With
the increase in temperature, the random motion of electrons increases. As a
result, the number of collisions of electrons with the positive ions increases
in a metal. Hence, the resistance of a metal increases with increase in
temperature.
The
resistance of the semiconductor substances decreases with an increase in
temperature. The resistivity of the semiconductor decrease exponentially with
an increase in temperature
The materials which offer very high resistance and restrict the
flow of electrons are called insulating materials. The insulating material has
widespread use in electrical applications for preventing leakage current Thus,
the resistance of the semiconductor and insulator decrease with an increase in
temperature.
(c) Differentiate the characteristics of electrical and electronics
systems. 05
Ans:
|
Basis For Comparison |
Electrical Device |
Electronics Device |
|
Definition |
It is defined as the device which uses the
electrical energy for performing the work. |
The device which controls the flow of electrons for
performing the particular task is known as the electronics devices. |
|
Material Used |
Metals like copper and aluminum are used for the
conduction of current. |
Semiconductor material like silicon, germanium etc. |
|
Operating Principle |
Convert the electrical energy into other forms of
energy. |
Uses the electrical energy for performing the
particular task. |
|
Current |
Alternating Current |
Direct Current |
|
Voltage |
Works on high voltage. |
Works on low voltage |
|
Power consumption |
More |
Less |
|
Manipulation |
Do not manipulate the data |
It manipulates the data. |
|
Response Time |
Fast |
Slow |
|
Required Space |
More |
Less |
|
Safe |
Less |
More |
|
Uses |
For doing mechanical work. |
For amplifying the weak signal or for coding and
decoding the information. |
|
Examples |
Transformer, motor, generator etc. |
Transistor, diode, microprocessor, flip-flop,
amplifier, etc. |
Q.3 (a) What is self and mutual inductance? Derive the
expression for co-
efficient of self and mutual inductance.06
Ans: Self-inductance is the property of the current-carrying coil
that resists or opposes the change of current flowing through it. This occurs
mainly due to the self-induced emf produced in the coil itself.
Mutual inductance is the opposition to
the change of current in one coil due to the presence of a second coil.
Expression for self
coefficient
We
are considering a solenoid with nn turns with length ll . The area of cross section is A.
The
solenoid carriers current I and B is the magnetic field inside the solenoid.
The magnetic field B is given as,
B=μ0nIl
Where, μ0 is
the permeability of free space, n is the number of turns and I is the current in the solenoid and L is the length.
The magnetic flux is the product of the magnetic field
and area of the cross section.
Here the magnetic flux per turn is given as,
ϕ=B×A
Substituting the values in the above expression,
ϕ=μ0nIl×A
Hence there is n number of turns, the total magnetic flux is
given as,
ϕ=(μ0nI×A×n)./L
ϕ=μ0n2IA/L..............(1)
If L is the coefficient of self-inductance of the
solenoid, then
ϕ=LI...........(2)
Comparing the two equations we get,
LI=μ0n2IA/L
L=μ0n2A/l
So the expression for the coefficient of
self-inductance is
μ0n2A/l
Mutual inductance
Let S1, and SS2 be two long solenoids of
length l. the solenoid S2is
wound closely over the solenoid S1as shown in the figure
below.
.
Let N
be the number of turns, B be the magnetic field and I be the current in the
solenoids
Therefore, we know that magnetic field of
solenoid S1
is
given by,
B1=μ0N1I1/l ……………
(1)
The
flux linked with solenoid
S2S2
is
given by,
ϕ2=B1AN2
Therefore, from (1)
We get,
ϕ2=(μ0N1lI1)A×N2………………..
(2)
But we know that,
ϕ2=MI1………………
(3)
Where, M is he coefficient of mutual inductance
Therefore, from (2) and (3)
We get,
MI1=μ0N1N2AI1/l
Therefore,
M=μ0N1N2A/l
Therefore, the coefficient of mutual inductance
between two given solenoids is
M=μ0N1N2A/l
(b) Derive the expression for energy stored in a
capacitor. 06
Ans: A
capacitive circuit is shown in the above figure. In a circuit, with voltage
around the capacitor V, the Capacitance C is given by the equation:
Q=CV…(1)
Where, Q represents the charge stored in the
capacitor.
Now, we want to find the energy stored in a capacitor.
According to electrostatics, the energy stored in a
capacitor will be equal to the work done to move the charge into the capacitor
having an electrical potential V.
Or
dW=VdQ…(2)
Now, for a capacitor, V=QC …(3)
So, we can put the value of V from equation (3) into
equation (2).
This gives,
dW=Q/CdQ,
Now the total work done to move charge Q can be found
by integration,
∫W0dW=1/C![]()
Now, from the integration method given in the formula
used section, we can calculate the following result.
W=1/2Q2C
, This is also equal to the energy
stored in the capacitor.
Therefore, U=0.5Q2/C
Moreover, from equation (1), we can put Q2=(CV)2
This will give us,
U=12Q2C
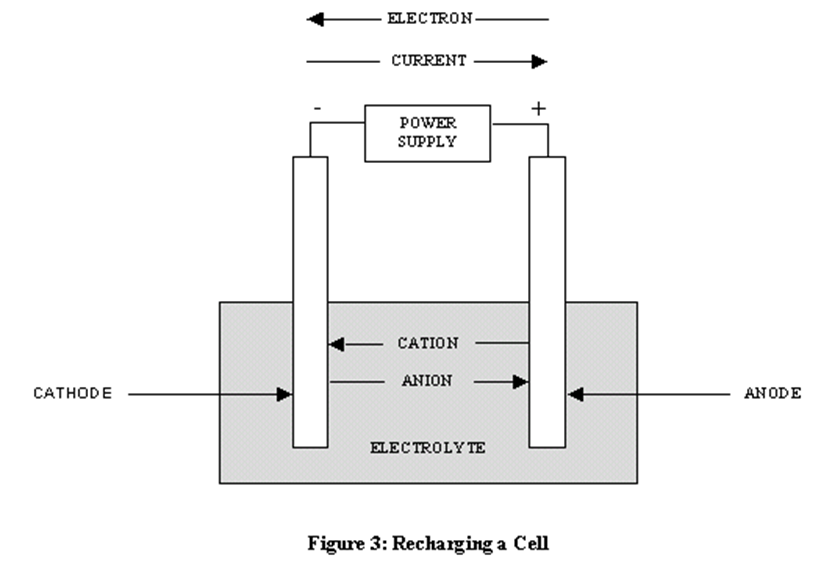
(c) What is cell? Classify different types of cells.
Discuss the grouping of
cells for higher voltage and higher current
requirements with
appropriate diagrams.
Ans: A primary cell or battery is one that cannot
easily be recharged after
one use, and are discarded following discharge. Most primary cells utilize
electrolytes that are contained within absorbent material or a separator (i.e.
no free or liquid electrolyte), and are thus termed dry cells.
A secondary cell or battery is one that can be electrically
recharged after use to their original pre-discharge condition, by passing
current through the circuit in the opposite direction to the current during
discharge. The following graphic evidences the recharging process.
Secondary batteries fall into two sub-categories depending on
their intended applications.
· Cells that
are utilized as energy storage devices, delivering energy on demand. Such cells
are typically connected to primary power sources so as to be fully charged on
demand. Examples of these type of secondary cells include emergency no-fail and
standby power sources, aircraft systems and stationary energy storage systems
for Load levelling
· Cells that
are essentially utilized as primary cells, but are recharged after use rather
than being discarded. Examples of these types of secondary cells primarily
include portable consumer electronics and electric vehicles.
Combination of Two or More Cells
There
are three types of combinations of cells:
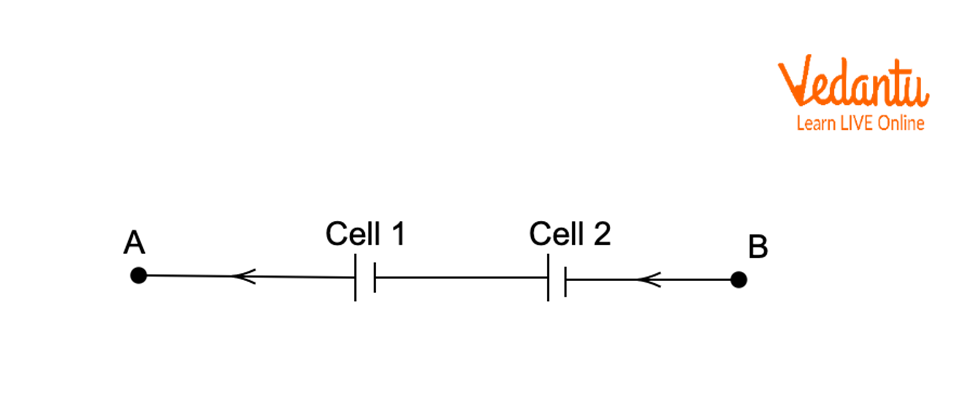
- Series
Combination: In a
series combination, all the cells are connected side by side. The current
through all the cells is the same. When two or more cells are connected in
series, the combination is called ‘Battery’.
Series Combination
- Parallel
Combination: In a
parallel combination, all the cells are connected in a parallel manner.
The voltage across all the cells may or may not be the same, depending
upon the nature of all the cells.
Parallel Combination
- Mixed
Combination: In a
mixed combination, some cells are in series and other cells are in
parallel.
Mixed Combination
Formula for Cells in Parallel
In
a parallel combination, the cells are connected in parallel form. Consider ‘n’
cells of emf E1, E2, E3,…, En and internal resistance
r1, r2, r3,…, rn connected in parallel
across a resistor of resistance ‘R’. The net current from all the cells will
add up at the junction and form the equivalent current.
Ieq=I1+I2+I3+...+In
Req=E1r1+E2r2+E3r3+...+Enrn
1Req=1r1+1r2+1r3+...+1rn
Formula for Cells in Series
In
a series combination, the cells are connected in series form or side by side.
Consider ‘n’ cells of emf E1, E2, E3,…, En and internal resistance r1, r2, r3,…, rn connected in parallel
across a resistor of resistance ‘R’.
The
value of current passing through all the cells will be the same. When two or
more cells are connected in series, the emf of all the cells add up and we get
a net emf. Also, since all the internal resistances are connected in series,
the resistances will add up and we will get a net resistance.
Eeq=E1+E2+E3+...+En
Req=r1+r2+r3+...+rn
Formula for Cells in Mixed Combination
In
a mixed combination, the cells are connected both in series and parallel
format. Consider ‘m’ rows in a parallel combination such that each row consists
of ‘n’ cells of emf ‘E’ and internal resistance ‘r’. Consider that the whole
combination is across an external resistance ‘R’. Here, ‘mn’ is a
constant.
In
this case, the current is given by I=mnEmR+nr.
Also,
the maximum current is drawn from the battery when external resistance matches
the net internal resistance. The maximum current is given by max=mE2r.
3.a.What
do you mean by statically and dynamically induced emf? Derive the expression
for co-efficient of coupling. 06
Ans: Induced EMF
When
a magnetic flux linking a conductor or coil changes, an electromotive force
(EMF) is induced in the conductor or coil, is known as induced EMF.
Depending upon the way of bringing the change in magnetic flux, the induced EMF
is of two types −
·
Statically Induced EMF
·
Dynamically Induced EMF
Statically Induced EMF
When
the conductor is stationary and the magnetic field is changing, the induced EMF
in such a way is known as statically induced EMF (as in a
transformer). It is so called because the EMF is induced in a conductor which
is stationary. The statically induced EMF can also be classified into two
categories −
·
Statically Induced EMF
·
Mutually Induced EMF
Self-Induced EMF
When
an EMF is induced in the coil due to the change of its own magnetic flux linked
with it is known as self-induced EMF.
Explanation −
When a current flows in a coil, a magnetic field produced by this current
through the coil. If the current in the coil changes, then the magnetic field
linking the coil also changes. Therefore, according to Faraday’s law of
electromagnetic induction, an EMF being induced in the coil. The induced EMF in
such a way is known as self-induced EMF.
Mathematically,
self-induced EMF is given by,
e=Ldidt...(1)
Where,
L is the self-inductance of the coil.
Mutually Induced EMF
When
an EMF is induced in a coil due to changing magnetic flux of neighbouring coil
is known as mutually induced EMF.
Explanation −
Consider two coils coil-1 and coil-2 placed adjacent to each other (see the
figure). A fraction of the magnetic flux produced by coil-1 links with the
coil-2. This magnetic flux which is common to both the coils 1 and 2 is known
as mutual flux (φm)(φm).
Now, if the current in coil-1 changes, the mutual flux also changes and thus
EMF being induced in both the coils. The EMF induced in coil-2 is known
as mutually induced EMF, since it is induced due changing in
flux which is produced by coil-1. Mathematically, the mutually induced EMF is
given by,
em=Mdi1dt...(2)
Where,
M is the mutual inductance between the coils.
Dynamically Induced EMF
When
the conductor is moved in a stationary magnetic field so that the magnetic flux
linking with it changes in magnitude, as the conductor is subjected to a
changing magnetic, therefore an EMF will be induced in it. The EMF induced in
this way is known as dynamically induced EMF (as in a DC or AC
generator). It is so called because EMF is induced in a conductor which is
moving (dynamic).
Explanation −
Consider a conductor of length l meters moving with a velocity
of v m/s at right angles to a uniform stationary magnetic field of flux density
B Wb/m2.Let the conductor moves
through a small distance dx in time dt seconds.
Then,
Area swept by conductor,a=l×dxm^2
∴Magnetic flux cut by conductor,dψ=Magnetic FluxDensity×Area Swept
⟹dψ=BldxWb
Now,
according to Faraday’s law of electromagnetic induction, the induced EMF will
be,
e=Ndψ/dt=Bldx/dt(∵N=1)
∵dx/dt=Velocity(V)
∴e=BlvVolts...(3)
Equation
(3) gives the dynamically induced EMF when the conductor moves at right angle
to the magnetic field.
If
the conductor moves at an angle &theta to the magnetic field, then the EMF
induced due to only the perpendicular component of the velocity to the magnetic
field.
e=Blvsinθ...(4))
(b)
Describe the charging and discharging action of capacitor with appropriate
voltage-charge characteristics. 06
Ans: Consider a capacitor connected in series with a resistor, to a
constant DC supply through a switch S.
‘C’ is the value of
capacitance and ‘R’ is the resistance value. The ‘V’ is the Voltage
of the DC source and ‘v‘ is the instantaneous voltage across the
capacitor.
When
the switch ‘S’ is closed, the current flows through the capacitor and it
charges towards the voltage V from value 0. As the capacitor charges, the
voltage across the capacitor increases and the current through the circuit
gradually decrease. For an uncharged capacitor, the current through the circuit
will be maximum at the instant of switching. And the charging currents reaches
approximately equal to zero as the potential across the capacitor becomes equal
to the Source voltage ‘V’.
Capacitor charging equation derivation
steps,
Considering
voltage law, the source voltage will be equal to the total voltage drop of the
circuit.
Therefore,
Rearrange
the equation to perform the integration function,
RHS
simplification,
On
integrating we get,
As we
are considering an uncharged capacitor (zero initial voltage), the value of
constant ‘K ‘ can be obtained by substituting the initial conditions of the
time and voltage. At the instant of closing the switch, the initial condition
of time is t=0 and voltage across the capacitor is v=0.
Thus we
get, logV=k for t=0 and v=0.
Taking
exponential on both sides,
From the above expression, it is clear that the instantaneous voltage will be a result of factors such as capacitance, resistance in series with the capacitor, time and the applied voltage value.
As
the value of the constant RC increases, the value of exponential function![]() also increases. That is the rate of voltage rise across the
capacitor will be lesser with respect to time. That shows the charging time of
the capacitor increase with the increase in the time constant RC.
also increases. That is the rate of voltage rise across the
capacitor will be lesser with respect to time. That shows the charging time of
the capacitor increase with the increase in the time constant RC.
As the
value of time ‘t’ increases, the term ![]() reduces and it means the voltage across
the capacitor is nearly reaching its saturation value.
reduces and it means the voltage across
the capacitor is nearly reaching its saturation value.
Charge q and charging current i of a capacitor
The
expression for the voltage across a charging capacitor is derived as,
ν = V(1- e -t/RC) → equation (1).
V – source voltage
ν – instantaneous
voltage
C– capacitance
R – resistance
t– time
The
voltage of a charged capacitor, V = Q/C.
Q– Maximum charge
The
instantaneous voltage, v = q/C.
q– instantaneous charge
q/C =Q/C (1-
e -t/RC)
q = Q (1- e -t/RC)
Charging current
For a capacitor, the flow of the charging current decreases
gradually to zero in an exponential decay function with respect to time.
From the voltage law,
ν = V(1- e -t/RC)
ν = V – V e -t/RC
V – ν = V e -t/RC →equation(2)
The source voltage, V = voltage drop across the resistor
(IR) + voltage across the capacitor ( ν ).
V = i R
+ ν
V – ν = i R
Substitute V – ν = i R in the
equation 2.
Therefore, i R
= V e -t/RC
i = (V
/R) e -t/RC
As V is the source voltage and R is the resistance, V/R will
be the maximum value of current that can flow through the circuit.
V/R =Imax
i = Imax e -t/RC
Capacitor Discharge Equation
Derivation
For a discharging capacitor, the voltage across the capacitor v discharges
towards 0.
Applying Kirchhoff’s voltage law, v is equal
to the voltage drop across the resistor R.
The current i through the resistor is rewritten as above and
substituted in equation 1.
By integrating and rearranging the above equation we get,
Applying exponential function,
The instantaneous voltage across a discharging capacitor is v = V
e -t/RC
Instantaneous charge, q = Q e -t/RC
Instantaneous current, i =
– Imax e -t/RC
From the above equations, it is clear that the voltage, current,
and charge of a capacitor decay exponentially during the discharge. The
discharge current has a negative sign because its direction is opposite to the
charging current.
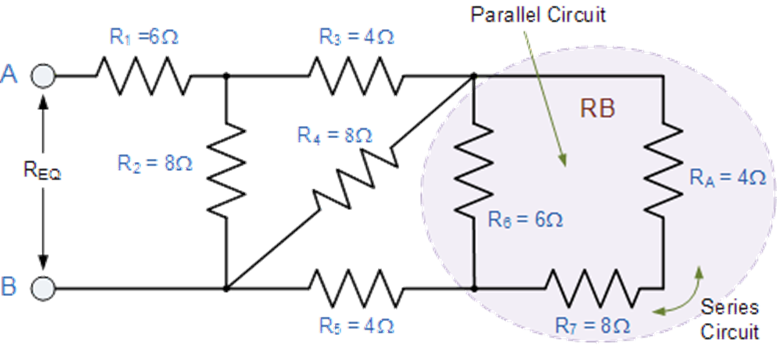
(c) Find
the equivalent resistance for the following resistor combination circuit. 06
Ans: Find the equivalent resistance, REQ for
the following resistor combination circuit.
Again, at first glance this resistor ladder network may seem a
complicated task, but as before it is just a combination of series and parallel
resistors connected together. Starting from the right hand side and using the
simplified equation for two parallel resistors, we can find the equivalent
resistance of the R8 to R10 combination
and call it RA.
RA is
in series with R7 therefore the total
resistance will be RA + R7 = 4 + 8 = 12Ω as shown.
This
resistive value of 12Ω is now in parallel with R6 and
can be calculated as RB.
RB is
in series with R5 therefore the total
resistance will be RB + R5 = 4 + 4 = 8Ω as shown.
This
resistive value of 8Ω is now in parallel with R4 and
can be calculated as RC as shown.
RC is
in series with R3 therefore the total
resistance will be RC + R3 = 8Ω as shown.
This
resistive value of 8Ω is now in parallel with R2 from
which we can calculated RD as:
RD is
in series with R1 therefore the total
resistance will be RD + R1 = 4 + 6 = 10Ω as shown.
Section 2
Q.4 (a) Select the most appropriate option. (Each of one mark) 06
1. Reciprocal of Power Factor = _________?
a. Demand Factor b. Diversity Factor c. Utilization Factor d. Q Factor Ans:D
For reading purpose only.






















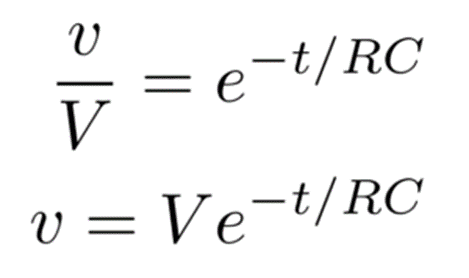



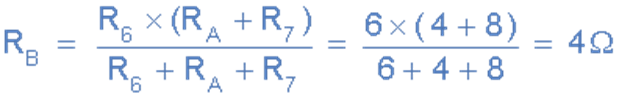





Comments
Post a Comment
Thank you for visiting😊